В.А. ХУДЯКОВ, канд. техн. наук, Л.В. ЛЕВИЦКАЯ, М.А. ГАВРИЛОВ, Н.Г. ЛЕСОВА, инженеры,
Пензенский государственный университет архитектуры и строительства
Рост числа предприятий химической промышленности сопровождается увеличением доли конструкций, подвергающихся воздействию азотной кислоты и оксидов азота. Низкая коррозионная стойкость большинства материалов обусловливает необходимость защитных мероприятий. Весьма эффективным является применение футеровок, выполненных на основе кислотостойких полимерных композиционных материалов (КМ) на термореактивных связующих.
К материалам для футеровок предъявляется ряд требований, связанных с прочностными показателями. Прежде всего это прочность при изгибе и сопротивление ударным нагрузкам. Известным недостатком КМ на основе термореактивных матриц (связующих) являются повышенная хрупкость и низкое сопротивление удару, что ограничивает область их применения.
Повышение сопротивления удару может быть достигнуто уменьшением степени сшивки полимера или за счет включения каучуковой фазы. Однако это приводит к снижению теплостойкости и некоторых прочностных показателей КМ [1, 2].
Дисперсное армирование короткими волокнами лишено указанных недостатков. Помимо того введение коротких волокон позволяет уменьшить усадку материала.
Для изготовления КМ в качестве армирующих волокон были использованы волокнистые отходы химической промышленности (ВОХП), представляющие собой тонкодисперсные волокна асбеста.
Матричный материал защитных КМ должен обладать также такими свойствами, как возможность отверждения без выделения побочных продуктов, адгезия к дисперсным фазам и подложке. Перечисленные требования делают целесообразным применение эпоксидных смол. В качестве дисперсных фаз КМ были использованы аморфный углерод как наполнитель и кварцевый
песок как мелкий заполнитель.
Улучшения реологических свойств композиции можно достичь не только пластификацией матричного материала, но и применением различных добавок. Особенно эффективны фторхлоруглеродные жидкости (ФХУЖ). Введение оптимальных количеств ФХУЖ помимо улучшения реологических свойств композиции приводит к получению КМ с повышенными физико-механическими свойствами и сниженной пористостью.
Для исследования влияния коэффициента армирования и концентрации ФХУЖ (по отношению к объему матричного материала) была выполнена серия экспериментов в соответствии с девятиточечным центральным композиционным планом для квадратичной модели. Основные уровни и интервалы варьирования действующих переменных определены по результатам предварительных исследований. Коэффициент армирования (объемная доля ВОХП по отношению к матричному материалу) варьировался в пределах [0; 0,2]; концентрации ФХУЖ – в пределах [0; 2]. В результате обработки эмпирического материала получены экспериментально-статистические (ЭС) модели для трех исследованных показателей (входные переменные даны в кодовом выражении).
Для определения предела прочности при сжатии ЭС-модель имеет вид (МПа):
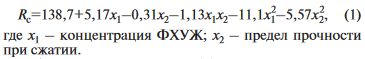
Абсолютная величина коэффициента при произведении действующих переменных сравнительно мала.
Это указывает на то, что в рассматриваемой области варьируемые факторы действуют практически независимо друг от друга. Модули коэффициентов при вторых степенях превосходят модули при первых; с удалением от центра плана значение прочности при сжатии падает. Изменение коэффициента армирования оказывает наиболее существенное влияние на прочность. Варьирование концентрации ФХУЖ, в особенности вблизи оптимальных значений коэффициента армирования, оказывает не столь выраженное влияние. Характер изменения прочности при увеличении коэффициента армирования выше оптимального значения можно объяснить снижением технологических свойств композиции и увеличением доли волокон, для которых характерно неполное смачивание матричным материалом.
Максимальное значение прочности, равное 139,3 МПа достигается вблизи центра плана (коэффициент армирования 0,12; концентрация ФХУЖ 0,9%).
Относительное упрочнение по сравнению с базовым составом (116 МПа) составляет 20%.
![]()
ЭС-модель для расчета предела прочности при изгибе (МПа):
Если на предел прочности при сжатии коэффициент армирования и концентрация ФХУЖ влияют независимо друг от друга, то для предела прочности при изгибе имеет место синергетический эффект в совместном влиянии варьируемых факторов. Коэффициент при произведении переменных положителен и по модулю близок к коэффициентам при вторых степенях. Увеличение концентрации добавки позволяет получить материал, который при бóльших коэффициентах армирования имеет лучшие прочностные показатели: максимальная прочность (29 МПа) достигается в точке, соответствующей коэффициенту армирования 0,15>0,12.
Относительное упрочнение по сравнению с базовым составом составляет 47%.
ЭС-модель для сопротивления ударным нагрузкамимеет вид (МДж/м3):
![]()
На значение сопротивления удару оказывают совместное влияние оба варьируемых фактора. При увеличении концентрации ФХУЖ выше оптимальной для сохранения высокого сопротивления удару требуется снизить коэффициент армирования, и наоборот. Влияние концентрации ФХУЖ на исследуемый показатель незначительно. Наибольшее сопротивление удару
(120,5 МДж/м3) достигается при коэффициенте армирования 0,17 и концентрации ФХУЖ 0,6%. Упрочнение по сравнению с базовым составом 44%.
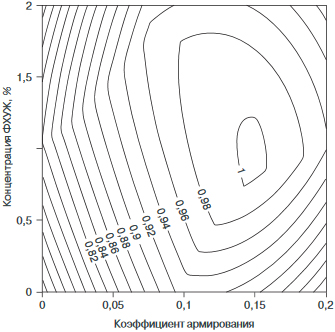
Для всех трех исследованных показателей оптимальные значения достигаются во внутренней части исследованной факторной области. Это свидетельствует о рациональном выборе интервалов варьирования действующих переменных. Очевидно, что, ожидая близость рецептур, соответствующих оптимальным значениям свойств «одного класса», например, физико-механических, не следует ожидать их совпадения. Разработанные методы решения применимы только для однокритериальных задач, поэтому реально достичь лишь некоторого компромисса, формальным выражением которого является целевая функция, количественно выражающая принятое в данной задаче понятие качества материала [3].
Для выполнения расчетов был выбран метод скаляризации введением целевой функции на основе неформально определенных контрольных показателей [3]. Результат оптимизации – подобласть допустимых рецептур исследованной факторной области, возможно, пустая. Точка, соответствующая экстремуму целевой функции, принадлежит этой подобласти. Достоинством метода является его гибкость: как правило, принятая в качестве оптимальной рецептура не соответствует точке экстремума целевой функции и выбирается исходя из дополнительных соображений (стоимость, технологические свойства композиции и т. д.).

Максимум целевой функции:
Контрольные показатели имеют смысл значений, определяющих границы области допустимых рецептур;
уравнение границ q(x1,x2) = 1. Для конкретной практической задачи примем в качестве контрольных: Rc*=138, Rb*=28 и Ri*=120. Изолинии (4) приведены на рисунке. Значения целевых функций полностью основаны на «первичных» полных квадратичных моделях (1)–(3), которые на уровне 0,05 адекватны полученным в эксперименте данным.
Максимум (4) достигается при коэффициенте армирования 0,15 и концентрации ФХУЖ 0,87%. Физико-механические свойства состава оптимальной рецептуры:
Предел прочности при сжатии, МПа . . . . . . . . . . . . . . . . .138,4
Предел прочности при изгибе, МПа . . . . . . . . . . . . . . . . . .28,14
Сопротивление удару, МДж/м3. . . . . . . . . . . . . . . . . . . . . .120,2
Непустая подобласть q(x1,x2) >1 свидетельствует о том, что армирование короткими волокнами в сочетании с введением модифицирующих добавок позволяет получить материал, обладающий показателями не ниже контрольных.