В.С. УТКИН, канд. техн. наук, Ж.В. КОШЕЛЕВА,
аспирант (Вологодский государственный технический университет)
Теория малой выборки является важнейшим направлением при оценке неопределенностей. В работе [1] был предложен новый метод оценки качества строительных материалов при малом количестве образцов на основе теории возможностей. Для этого была использована функция распределения возможностей (ФРВ) вида
![]()
где параметр а можно рассматривать как среднее значение качества, например прочности, определяемое по результатам испытания {X1, X2,…, Xn} в виде a=0,5(Xmax+Xmin). Параметр b (b=0,5(Xmax-Xmin)/εα, умноженный на
![]()
можно по аналогии с теорией вероятностей назвать половиной ширины доверительного интервала. a называется уровнем среза или уровнем риска, которым при оценке задаются качества материалов. Если ширина доверительного интервала зависит от того, каким значением уровня риска задаются, это отражает субъективность оценки качества материала. По воле испытателя некачественный материал можно перевести в разряд качественных субъективной заменой одного значения a на другое.
Приведем пример. Пусть по результатам испытаний трех бетонных кубиков на сжатие получены значения разрушающих напряжений, Xmax=30 МПа, Xmin=20 МПа. Найдем прочность бетона при сжатии, используя ФРВ [1]. Определяем параметры ФРВ

Определим, какова возможность того, что прочность бетона будет равна 23 МПа. Принимаем x = 23 МПа. Так как x = 23 < a = 25 МПа, то в обоих случаях возможность того, что прочность бетона будет 23 МПа равна 1.
Необходимость этого утверждения определяется из выражения N = 1-Q, где Q — возможность того, что прочность не равна 23 МПа. Так как x<a, то Q по (1) равна лх(х). Так, в нашем примере
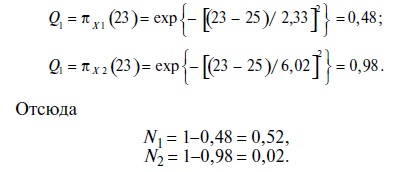
Следовательно, возможность того, что прочность бетона равна 23 МПа, находится в интервалах [0,52; 1] и [0,02; 1] соответственно для принятых а^=0,01 и а2=0,5. Из приведенного примера видно, что не наложив каких-либо ограничений на выбор уровня риска а, нельзя получить надежный результат.
Мерой неопределенности в примере выступает не вероятность, а возможность в интервальном виде, где различают верхнюю P и нижнюю P вероятности. При этом верхняя вероятность P при предполагаемой прочности материала, меньшей среднего значения а, равна P = 1 [1]. А нижнее значение вероятности в этом случае равно P = 1−πX(x), где πX(x) принимается в виде типовой функции (1).
Чтобы избежать выявленной неоднозначности в оценке качества строительных материалов, необходимо на значения а наложить ограничительные условия. В отечественных и зарубежных литературных источниках нам не удалось найти такие условия. В связи с этим были проведены многочисленные испытания бетонных и деревянных стандартных образцов на сжатие до разрушения.
Выбирая случайным образом образцы из совокупности в виде выборок различного объема от n = 1 до n = 50 и проводя обработку результатов испытаний по теории вероятностей и теории возможностей, мы установили следующее. При малом числе образцов (n<10) наблюдалась неустойчивость значений средних арифметических и среднеквадратических отклонений, определяемых методами теории вероятностей, что указывает на ее неприменимость. Тогда математическую обработку результатов испытаний провели методами теории возможностей и нашли параметры а и b функции (1). Так как b зависит от а, то значение его подбирали из построенных графиков Р= 1 и P = 1−πX(x) теории возможностей и графиков различных известных функций распределения теории вероятностей.
| n | a |
| 2 | 0,64 |
| 3 | 0,501 |
| 4 | 0,402 |
| 5 | 0,325 |
| 6 | 0,262 |
| 8 | 0,163 |
| 9 | 0,122 |
Известно [2], что по аксиоме теории возможностей все функции теории вероятностей должны находиться в интервале функций [P, P] при любой прочности материала, то есть P < P < р. В результате обработки экспериментальных данных, построения ФРВ и функций распределения вероятностей удалось найти зависимость между значением а и различным числом образцов в выборках (n = 1,…,9), которая описывается прямой в полулогарифмических осях координат (lnn, а), полученной по теории наименьших квадратов в виде α = A + B · lnn,, где число образцов n<10. Параметры A и B для различных пород древесины (ель, сосна, ольха) колеблются соответственно A от 0,87 до 0,89 и B от -0,33 до -0,36 при n>10 а = 0. С уменьшением числа образцов значение а увеличивается. Значения а находятся в интервале [0,1] и зависят от числа образцов n<10.
Таким образом, при оценке качества строительных материалов значение уровня риска должно быть согласовано с объемом выборки n. Для исследованных пород древесины значения а при различном числе n образцов приведены выше.
При сравнении материалов по тому или иному показателю качества значение а принимается любое, но одно и то же, при одном и том же объеме выборки, то есть сравнение проводится всегда с одним уровнем риска.
Ограничительные условия при выборе значения уровня риска а не являются недостатком нового метода определения качества строительных материалов, так как подобная неопределенность имеет место и при больших выборках, когда применяются методы теории вероятностей, в частности интервальная оценка в виде доверительного интервала. Ширина доверительного интервала, как известно, зависит от выбора значения доверительной вероятности или уровня значимости а, и различия показателей качества могут быть существенными.
Преимущество нового метода оценки качества материала заключается в том, что он разработан и проверен экспериментально для малых по объему выборок, когда вероятностные методы неприменимы.
Список литературы
- Уткин В.С. Оценка качества строительных материалов при малом числе образцов // Строит. материалы, 2001. № 1. С. 32-33.
- Дюбуа Д., Прад А. Теория возможностей. Приложения к представлению знаний в информатике. М.: Радио и связь, 1990. 288 с.
Статья взята из журнала «Строительные материалы»